6270. Дети в Дружественном Классе

Кевин помнит свой класс в начальной школе. В его классе Были девочки и мальчики. Некоторые из них были друзьями, а некоторые и нет. Но если один человек является другом другому, то обратное утверждение также верно.

Интересно, что каждая девочка имеет в точности a друзей среди девочек и точно b друзей среди мальчиков, в то время как каждый мальчик имеет в точности с друзей среди девочек и ровно d друзей среди мальчиков.

Кевин не помнит количество детей в классе. Помогите ему восстановить класс с минимальным возможным числом детей таким образом, чтобы все вышеуказанные условия были удовлетворены.

Вход. Четыре целых числа a, b, c и d (1 ≤ a, b, c, d ≤ 50).

Выход. Выведите пример класса с минимальным количеством детей, удовлетворяющего выше перечисленным условиям.

В первой строке выведите два натуральных числа: m – количество девочек, и n – количество мальчиков.

Присвоим числа от 1 до m девочкам, а от m + 1 до m + n – мальчикам.

Каждая следующая строка должна содержать пару различных чисел, описывающих пару друзей. Каждую пару друзей следует вывести только один раз.

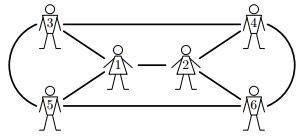
Пример входа	Пример выхода
1 2 1 2	2 4 1 2 1 3 1 5 2 4 2 6 3 4 3 5 4 6 5 6

РЕШЕНИЕ

математика + перебор

Анализ алгоритма

Пусть в классе имеется m девочек и n мальчиков.

Составим соотношения между указанными значениями.

1. Пусть между девочками и мальчиками имеется k ребер. Из каждой девочки к мальчикам исходит b ребер (k = m * b). Из каждого мальчика к девочкам исходит c ребер (k = n * c). Следовательно m * b = n * c.

2. Пусть между девочками имеется l ребер. Из каждой девочки к остальным девочкам исходит a ребер. При этом каждое ребро считается дважды (l = m * a / 2). То есть произведение m * a должно быть четным. Аналогично произведение n * d также будет четным.

3. Поскольку из каждой девочки к остальным девочкам исходит a ребер, то m ≥ a + 1. Аналогично n ≥ d + 1.

Следует полным перебором найти такие m и n, удовлетворяющие всем указанным условиям, и выбрать пару, для которой m + n минимально.

Теперь следует найти хотя бы один допустимый вариант дружбы.

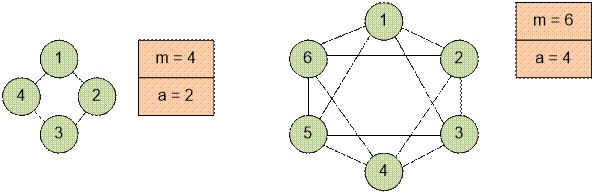
1. Девочка – Девочка. В классе имеется m девочек, каждая девочка дружит с a другими.

· Пусть a четно. Поставим в дружбу девочке с номером i девочек со всеми такими j, что i + 1 ≤ j ≤ i + 1 + (a / 2). Причем если значение j становится большим m, то положим j = (j – 1) % m + 1 (циклическая нумерация: i + 1, i + 2, …, m, 1, 2, …, (i + (a / 2)) % m + 1).

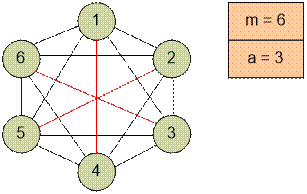
· Пусть a нечетно. Тогда исходя из того, что m * a должно быть четным, следует что m четно. Построим граф как в случае четного a, в результате чего получим что каждая девочка дружит с (a – 1) другой девочкой. Еще для каждой девочки не хватает по одной для дружбы. Поставим в дружбу девочке i (1 ≤ i ≤ m / 2) девочку с номером i + m / 2.

2. Мальчик – Мальчик. Действуем аналогично девочкам, строя симметричный граф.

3. Девочка – Мальчик. Пусть девочке с номером 1 поставили в соответствие мальчиков из интервала [1; b]. Тогда девочке с номером 2 поставим в соответствие мальчиков из интервала [b + 1; 2b]. Третьей девочке ставим мальчиков с номерами из интервала [2b + 1; 3b] и так далее. Номера мальчиков считаем циклически: 1, 2, …, n, 1, 2, …., n, 1, 2, … .

Реализация алгоритма

Читаем входные данные.

scanf("%d %d %d %d", &a, &b, &c, &d);

Полным перебором ищем значения m и n, минимизируя сумму m + n.

int ResM = 12345, ResN = 12345;

for (m = a + 1; m <= 52 * 52; m++)

for (n = d + 1; n <= 52 * 52; n++)

if (m * b == n * c)

if (((m * a) % 2 == 0) && ((n * d) % 2 == 0))

if ((m >= c) && (n >= b))

if (m + n < ResM + ResN)

{

ResM = m;

ResN = n;

}

int m = ResM, n = ResN;

Выводим количество девочек и мальчиков в классе.

printf("%d %d\n", m, n);

Выводим отношения дружбы между девочками.

// Girl - Girl

for (i = 1; i <= m; i++)

for (j = i + 1; j <= i + (a / 2); j++)

printf("%d %d\n", i, (j - 1) % m + 1);

if (a % 2 == 1)

for (i = 1; i <= m / 2; i++)

printf("%d %d\n", i, m / 2 + i);

Выводим отношения дружбы между мальчиками.

// Boy - Boy

for (i = 1; i <= n; i++)

for (j = i + 1; j <= i + (d / 2); j++)

printf("%d %d\n", m + i, m + (j - 1) % n + 1);

if (d % 2 == 1)

for (i = 1; i <= n / 2; i++)

printf("%d %d\n", m + i, m + n / 2 + i);

Выводим отношения дружбы между девочками и мальчиками.

// Girl - Boy

int BoyId = 0;

for (int i = 1; i <= m; i++)

for (int j = 1; j <= b; j++)

{

if (++BoyId > n) BoyId = 1;

printf("%d %d\n", i, m + BoyId);

}